Oscillateur de Pierce & oscillateur en pi
 L’oscillateur de Pierce dont le schéma est donné sur la figure 1 ci-contre se retrouve dans de très nombreux systèmes électroniques : qu’il s’agisse de votre montre (à quartz) en passant par votre téléphone portable, jusqu’à votre machine à laver on rencontre ce type d’oscillateur pour fournir l’horloge de fonctionnement des systèmes numériques. Pour la réalisation de l’amplificateur utilisé dans l’oscillateur de Pierce on retrouve une porte logique détournée.
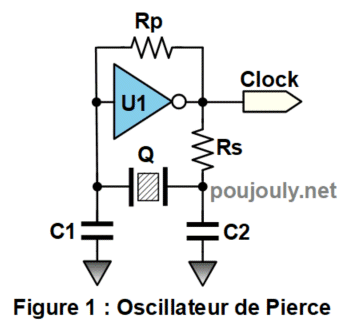
L’oscillateur de Pierce dont le schéma est donné sur la figure 1 ci-contre se retrouve dans de très nombreux systèmes électroniques : qu’il s’agisse de votre montre (à quartz) en passant par votre téléphone portable, jusqu’à votre machine à laver on rencontre ce type d’oscillateur pour fournir l’horloge de fonctionnement des systèmes numériques. Pour la réalisation de l’amplificateur utilisé dans l’oscillateur de Pierce on retrouve une porte logique détournée.
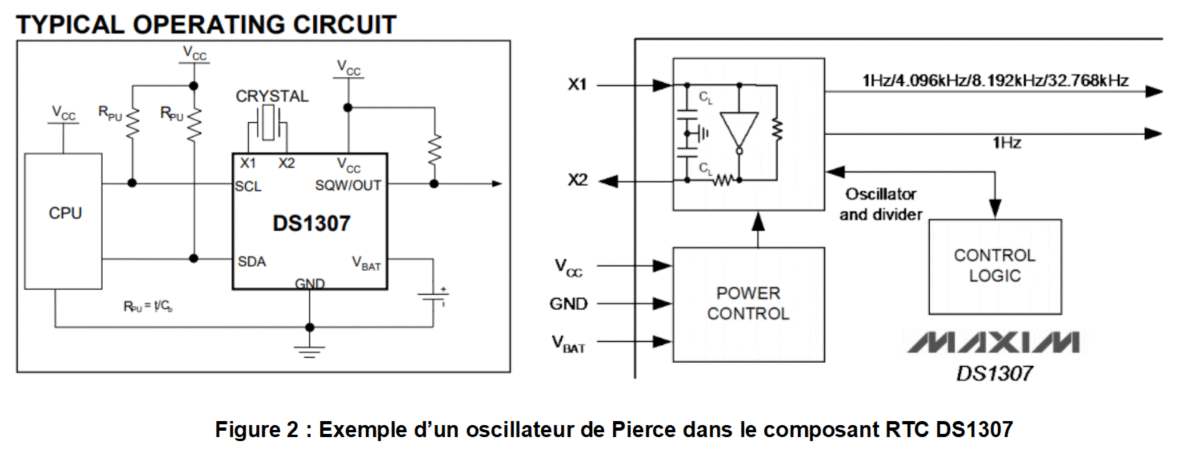
La figure 2 suivante est extraite d’une documentation du constructeur MAXIM pour le circuit DS1307 qui est une horloge temps réel communicant sur un bus I2C mettant en œuvre un quartz à 32,768kHz permettant d’obtenir une base de temps précise pour le comptage horaire et journalier. On retrouve bien évidemment la structure de l’oscillateur de Pierce.
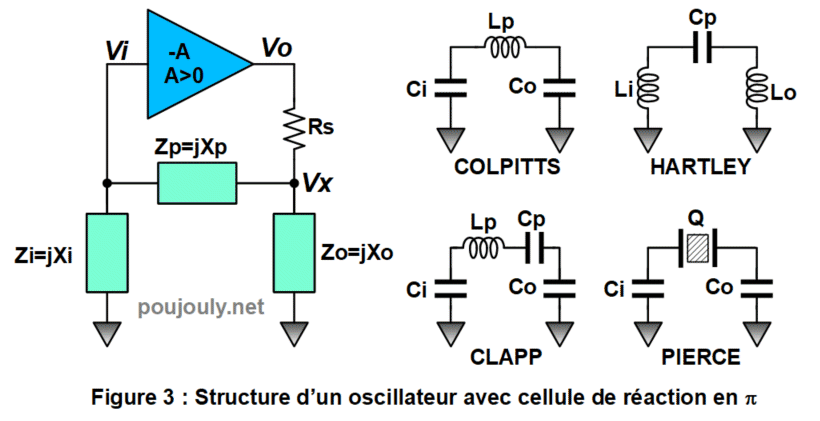
L’oscillateur de Pierce est un cas particulier des oscillateurs dont la boucle de réaction est une cellule en pi. En fonction de la configuration on retrouve plusieurs type d’oscillateurs utilisant à chaque fois des éléments réactifs (L, C,..) dans les branches de cette cellule comme l’indique la figure 3.
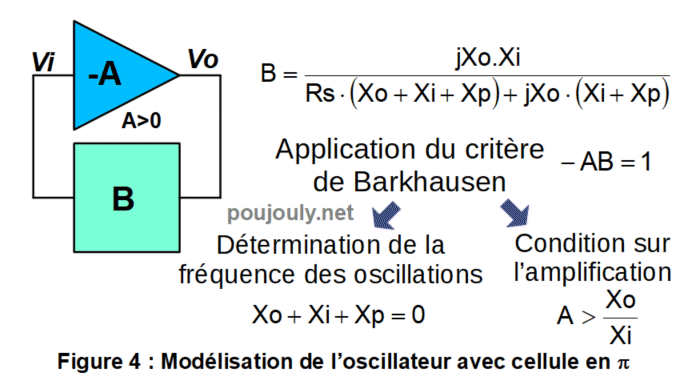
On peut alors modéliser cet oscillateur sous la forme indiquée sur la figure 4 ci-dessous dans laquelle on montre que la détermination de la fréquence des oscillations s’obtient très simplement en résolvant l’équation Xo+Xi+Xp=0.
Si l’on prend l’exemple d’un oscillateur de type Colpitts on obtient facilement l’expression de la fréquence des oscillations sur la figure suivante.
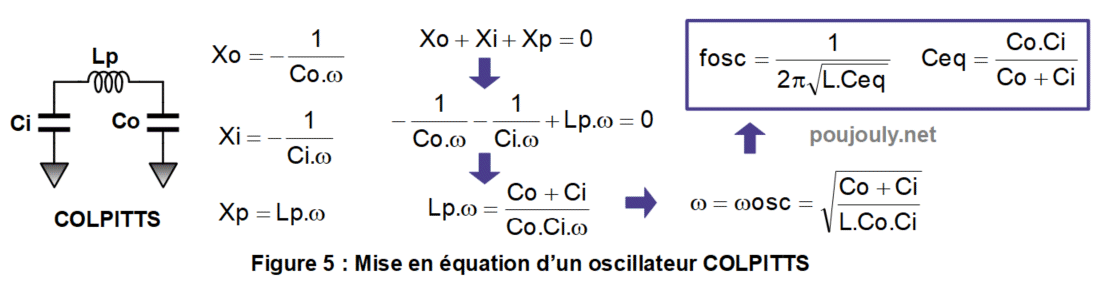
Comme l’on s’intéresse ici à un oscillateur utilisant un quartz il convient d’analyser l’impédance de ce composant.
Certains matériaux anisotropes comme le quartz présentent la propriété de se polariser électriquement lorsqu’on les comprime : cet effet est appelé piézo-électrique. Cet effet est aussi réversible, c’est à dire qu’une lame (ou cristal) d’un tel matériau subi des déformations lorsque l’on applique un champ électrique. En fixant des électrodes de part et d’autre du cristal, on forme ainsi un résonateur mécanique. L’application d’une tension provoque une excitation mécanique qui entraîne un déplacement de charges et donc la création d’un courant. Ce dipôle peut être modélisé par le schéma équivalent suivant au voisinage de la fréquence de résonance du cristal ce qui permet ainsi d’observer l’évolution de l’impédance en fonction de la fréquence.
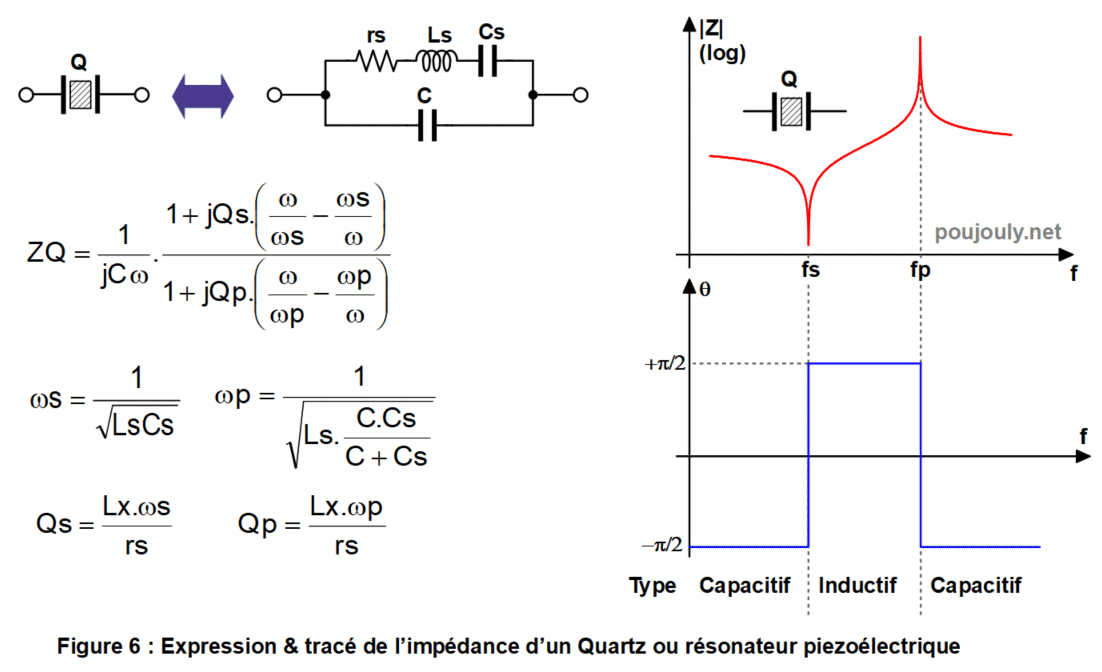
Si l’on suppose que les pertes d’un quartz sont négligeables la recherche de la fréquence des oscillations est alors obtenue en résolvant l’équation XQ+Xi+Xo=0. Cette équation peut alors se traduire graphiquement sur le tracé disponible sur la figure 7 suivante.
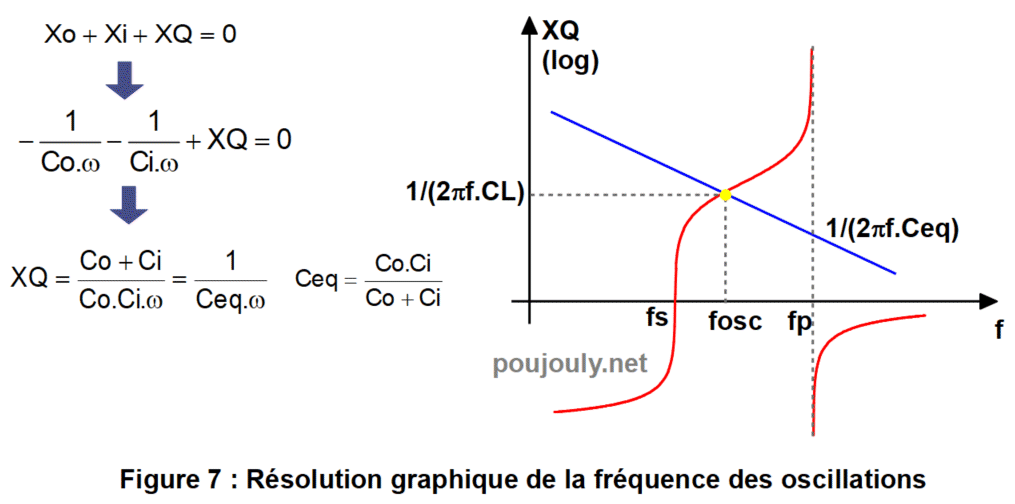
Lorsqu’on utilise un quartz le constructeur précise toujours la capacité de charge qui permet d’obtenir la fréquence des oscillations qui se trouve entre fs & fp. Pour un quartz les fréquences fs et fp sont excessivement proches bien évidemment.
En faisant varier les capacités Ci & Co on obtient de très légères variations de la fréquence des oscillations. C’est sur ce principe que fonctionne les VCXO (Voltage Controled Xtal Oscillator) en utilisant bien évidemment des diodes Varicap.
Traditionnellement on utilise 2 capacités Ci & Co identiques ce qui permet d’obtenir le démarrage des oscillations assez rapidement car la condition sur l’amplification est alors largement respectée (A>1).
- Télécharger cet article au format pdf : Oscillateur de Pierce et Oscillateur en pi.pdf
Laisser un commentaire